컴퓨터 성능의 측정 지표
1. Response Time ( Execution time, Latency)
특정한 작업을 시작해서 끝낼 때까지 걸린 시간을 측정한다.
개개인의 유저가 중요하게 생각하는 지표이며, 임베디드 컴퓨터와 개인용 컴퓨터는 response time 을 중요하게 생각한다.
2. Throughput
정해진 시간동안 처리하는 일의 양을 측정한다.
데이터센터나 슈퍼컴퓨터 관리자들이 중요하게 생각하며, '서버' 는 스루풋을 중요하게 여긴다.
컴퓨터 머신의 종류와 사용처에 따라 중요하게 생각하는 지표가 다르다.
(쓰루풋을 단순히 response time 의 역수로 생각할 수는 없다.)
Example
한번 다음과 같은 과정을 거쳐 빨래를 한다고 해보자.

세탁기는 30분, 건조기는 40분, 빨래를 개는데 20분이 걸린다고 하자.
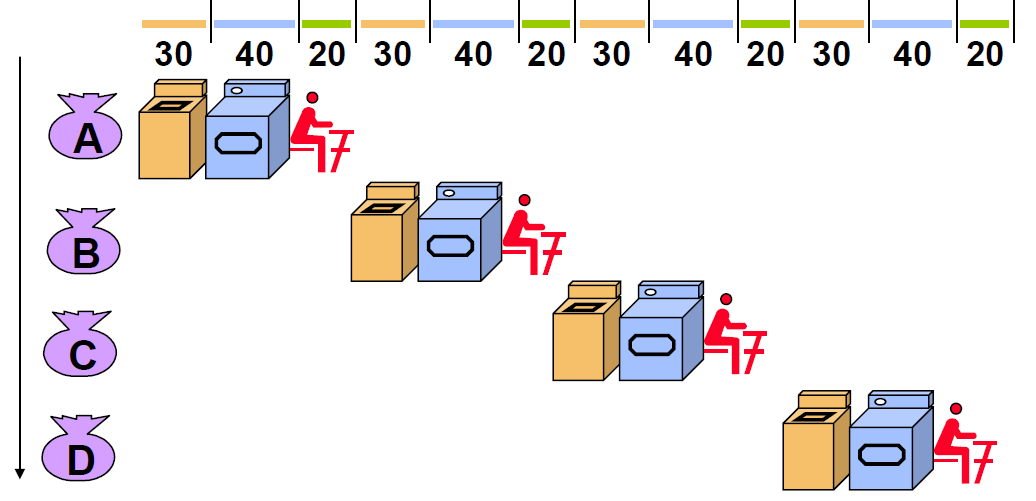
만약 4명의 사람들이 순차적으로 이 작업을 수행한다면 총 소요시간은 90분 x 4 = 360 분이다.
한명의 빨래를 끝내는데에는 90분의 시간이 걸렸으므로, Response Time = 90 min 이다.
그리고 360분동안 빨래를 4 Cycle 돌렸으므로, Throughput (1시간에 수행한 빨래 Cycle의 양)은 2/3 이다. (0.67 task / hr )
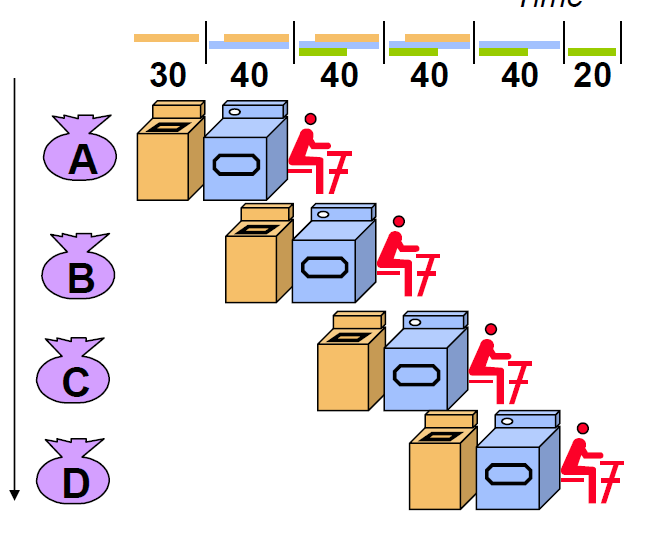
반면 각 단계를 파이프라인화 시켜서 빨래, 건조, 빨래 개기를 동시에 진행하면 다음과 같이 줄어든다.
빨래를 하나 끝내는데는 여전히 90분의 시간이 걸렸으므로, Response Time = 90 min 으로 동일하다.
반면 전체 4개 빨래 사이클을 끝내는데는 210분의 시간이 걸렸으므로, Throughput은 1.14 task / hr 이다.
Response Time 은 동일한데, Throughput 이 서로 다르게 나온다는 것을 알 수 있다.
파이프라인은 개별 사이클 (Response Time) 을 줄이는데 효과적이지 않지만, 전체 프로세스를 수행하는 시간을 줄이는데 효과적이다. (Throughput 개선)
단, 파이프라인 기법으로 효과를 보려면 각 stage 의 시간 간격차이가 크지 않아야 한다. (밸런스가 맞아야 한다.)
만약 세탁과 빨리 개기는 지금과 동일한데, 건조에는 4시간이 걸린다면 파이프라인으로 큰 효과를 볼 수 없다.
파이프 라인방식으로 동시에 진행할 수 있는 최대 일의 개수는 하나의 task를 쪼갠 stage의 개수와 동일하다.
따라서 stage를 잘게 나누면 나눌수록 전체 task 수행 시간이 더 줄어들 여지가 있다.
Performance 측정
지금까지 측정기준 2가지를 보았다.
하지만 이제부터는 Response Time 이라는 기준 하나에만 집중해서 보기로 하자.
컴퓨터의 성능을 측정하는 방법은 다양하게 있겠지만, 한번 간단하게 '프로그램의 실행시간이 빠를 수록 더 성능이 좋다' 라고 정의해보자.
그러면 아래와 같은 식으로 단순하게 표현할 수 있을 것이다.
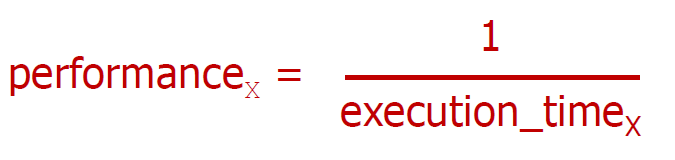
만약 이 식을 만족할 때, 서로 다른 두 컴퓨터의 성능은 아래와 같이 비교할 수 있다.
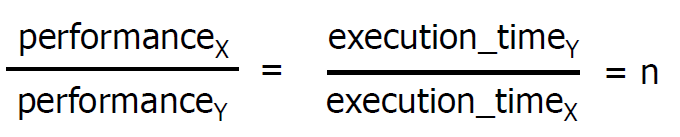
컴퓨터 x가 컴퓨터 y보다 n배 성능이 더 좋을 때, 그 n의 값은 위와 같이 계산할 수 있다.
이 공식을 이용하여 아래와 같은 예제 문제를 풀어보자.
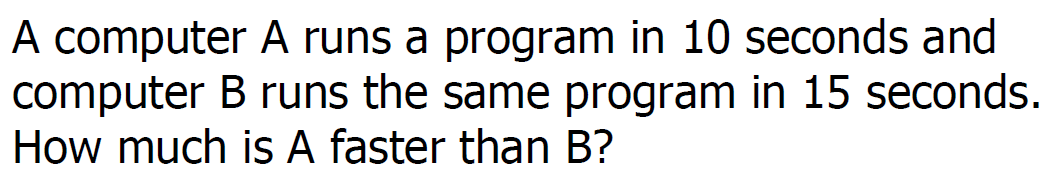
컴퓨터 A 가 프로그램 하나를 실행시키는데 10초가 걸린다.
만약 컴퓨터 B가 같은 프로그램을 실행시키는데 15초가 걸린다면, A는 B보다 얼마나 더 빠른가?
A 컴퓨터의 성능은 1/10, B 컴퓨터의 성능은 1/15
A 컴퓨터의 성능으로 B 컴퓨터의 성능을 나누면, 15 / 10 = 1.5
따라서 A 컴퓨터는 B 컴퓨터보다 1.5 배 빠르다.
Execution Time 측정
컴퓨터의 성능 performance를 측정할 때 위와 같이 실행시간을 이용하여 계산하기로 정의했다면
과연 실행시간은 어떻게 측정할 수 있을까?
전체 실행시간은 디스크 접근, 메모리 접근, I/O 작업, 운영체제 오버헤드 등 여러 시간들의 총합으로 결정된다.
하지만 정말 단순하게 CPU time만으로 실행시간을 계산해보자.
CPU time 은 CPU 가 하나의 주어진 작업을 처리하는데 걸리는 시간이다.
이렇게 계산한다면, 단순히 CPU time 이 작을 수록 더 좋은 성능의 컴퓨터라는 것을 알 수 있다.
CPU Clock
모든 컴퓨터는 CPU 가 가진 자체 시간 체계에 맞춰 작업을 수행한다.
따라서 CPU Time 을 사람이 사용하는 시간 체계인 '초' 에 맞추지 않고 이 클락 사이클이 몇번 지속됐느냐로 표현할 수도 있다.
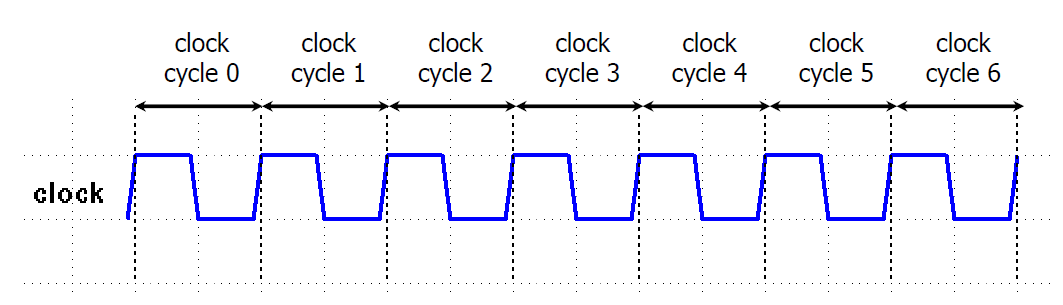
클락 사이클은 위와 같은 0과 1이 반복되는 파형이다.
파형이기 때문에, 물리에서 사용하는 '주기' 와 '주파수' 의 개념을 그대로 사용할 수 있다.
Clock 의 주기(Period)는 하나의 클락 사이클에 소요되는 시간이다.
Clock 의 주파수 (Frequency) 는 1초에 클락사이클이 반복되는 횟수이다.
주기의 역수로 표현한다.
만약 주기가 500ps라면 500ps = 0.5ns = 500 x 10^(-12)s 이다.
이 주기를 가진 CPU의 주파수는 이를 역수로 취하면 10^12 / 500 = 2 * 10^12 / 10^3 = 2 * 10^9 = 2GHz
CPU time을 이제 제대로 나타내보자.
우리는 CPU Time 을 위 개념을 이용하여 아래와 같이 정의할 수 있다.

CPU Time 은 정해진 횟수의 사이클이 돌아가는데 걸린 총 시간을 의미한다.
만약 어떤 프로그램이 다 실행되는데, 100개 사이클이 필요하다면, CPU Time 은 (100 * 주기) 가 될 것이다.
Example
만약 2GHz의 주파수를 가진 CPU로 돌아가는 컴퓨터 A가 어떤 프로그램을 실행시키는데 10초의 CPU Time 이 걸렸다고 해보자.
이때 같은 프로그램을 실행시키는데 6초가 걸리는 컴퓨터 B를 만들고자 한다.
그런데 같은 프로그램을 실행시키는데, 필요한 사이클의 수가 A컴퓨터의 1.2 배라고 하자.
그렇다면 이때 컴퓨터 B의 주파수는 어떻게 되어야할까?
굉장히 복잡해보이지만 하나씩 차근차근 계산해보자.
컴퓨터 A의 성능으로 프로그램을 실행시키는데, 필요한 총 Cycle의 수는 얼마일까?
CPU Time = Cycle 수 * 주기 = Cycle 수 / 주파수 이다.
따라서 10 = Cycle 수 / 2 = 20 Cycle 이 필요하다.
컴퓨터 B는 같은 프로그램을 실행시키는데, 1.2배의 사이클 수가 필요하다고 하였으므로, 20 * 1.2 = 24 개의 사이클이 필요하다.
컴퓨터 B는 24개의 사이클을 실행시키는데, 6초의 시간이 걸려야 한다. 따라서 다음과 같이 식을 작성할 수 있다.
6초 = 24개 사이클 * 주기 = 24개 사이클 / 주파수
따라서 주파수는 24 / 6 = 4GHz
CPI (Clock cycle Per Instruction)
프로그램은 결국 여러개의 명령어로 구성된 집합체이다.
따라서 프로그램을 실행시키는 컴퓨터의 성능은 이 명령어의 개수와 밀접하게 관련된다.
이때 CPU의 사이클은 결국 명령어를 처리하기 위해 필요한 하나 하나의 단계라고 볼 수 있다.
따라서 프로그램을 실행시키는데 필요한 총 Cycle 의 수는, 해당 프로그램이 갖는 명령어의 개수 x 명령어 하나를 실행시키는데 필요한 Cycle의 수로 계산할 수 있다.
명령어 하나를 실행시키는데 필요한 Cycle 의 수를 Clock cycle Per Instruction 이라고 하여 CPI 라고 부르며, 아래처럼 나타낼 수 있다.

위 공식에서는 Avg 즉, 평균 CPI 를 적었다.
평균값을 넣은 이유는, 명령어마다 CPI가 다를 수 있기 때문이다.
이를 총 정리하면
CPU Time은 아래와 같이 계산된다.
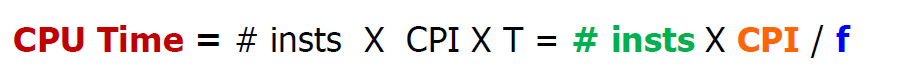
Example
컴퓨터 A, B 가 있다.
두 컴퓨터의 ISA는 같지만 제조사가 달라서 디테일한 구현이 다르다.
컴퓨터 A는 250ps 의 주기를 갖고 있고, 어떤 프로그램을 실행시킬 때 2.0 의 평균 CPI 를 갖는다.
컴퓨터 B는 500ps 의 주기를 갖고 있고, 어떤 프로그램을 실행시킬 때 1.2 의 평균 CPI 를 갖는다.
어떤 컴퓨터가 얼마나 더 빠를까?
당연히 직관적으로 봤을 때, A의 주기는 B의 1/2 인데 반해 CPI 는 2배 차이가 나지 않으니 A가 더 빠르다.
하지만 수학적으로 디테일하게 계산해보자.
두 컴퓨터 모두 같은 프로그램을 실행시키고 있으니, 프로그램의 명령어 개수는 똑같이 10개라고 하자.
그러면 컴퓨터 A는 2.0 * 10 = 20 개의 사이클을 실행해야 하고, 컴퓨터 B는 1.2 * 10 = 12 개의 사이클을 실행해야한다.
컴퓨터 A는 20 개 사이클을 실행할 때, 주기가 250ps = 0.25 ns = 250 x 10 ^ (-12) s 가 걸린다.
이를 주파수로 환산하면 4GHz 이다.
따라서 컴퓨터 A의 CPU Time 은 20 / 4GHz = 5s 이다.
컴퓨터 B의 경우에는 12개의 사이클을 실행할 때, 주기가 500ps 이므로 주파수는 2GHz이다.
따라서 CPU Time은 12 / 2GHz = 6s 이다.
이제 실행시간을 구했으니 성능을 비교할 수 있다.
성능은 시간의 역수로 정의했으므로, 컴퓨터 A 가 컴퓨터 B보다 1.2배 더 빠르다는 것을 계산할 수 있다.
(복잡하게 계산했지만, 사실 CPI 와 주기를 곱하면 명령어 하나를 실행하는데 필요한 시간이 나온다.)
CPI 와 성능
CPI 와 성능에 대해 조금 더 자세히 생각해보자.
과연 CPI 가 작을 수록 더 성능이 좋다고 말할 수 있을까?
컴퓨터가 실행하는 프로그램은 다양한 종류의 명령어로 이루어져있고, 각 명령어마다 실행되는데 필요로하는 Cycle 의 수는 다를 수 있다.
그래서 컴퓨터 성능을 측정할 때 '평균' CPI 를 이용해서 측정했었다.
하지만 '평균' CPI 가 더 작다고 해서 반드시 더 빠르다는 보장은 할 수 없다.
아래 예시를 보자.
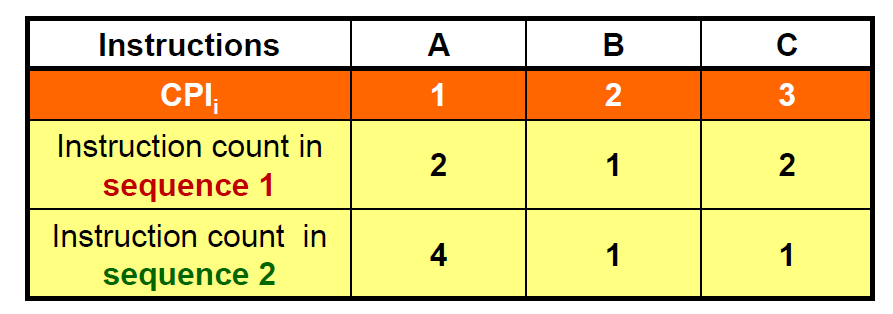
하나의 컴퓨터가 있고, 이 컴퓨터에서 돌아갈 프로그램을 만드는 2개의 컴파일러가 있다고 하자.
컴파일러 A는 sequence 1 의 조합으로 프로그램을 번역했고
컴파일러 B는 sequence 2 의 조합으로 프로그램을 번역했다.
이때 각 명령어별로 CPI 가 위 표와 같을 때, 각 컴파일러가 만든 프로그램의 실행시간은 어떻게 될까?
컴파일러 A가 만든 프로그램을 실행하는데 필요한 총 Cycle의 수는 1*2 + 2*1 + 3*2 = 10
컴파일러 B가 만든 프로그램을 실행하는데 필요한 총 Cycle의 수는 1*4 + 2*1 + 3*1 = 9
같은 컴퓨터는 Cycle 을 실행시키는 시간이 같으므로, 컴파일러 B가 만든 프로그램이 더 빠르게 동작한다.
평균 CPI 를 계산했을 때는 컴파일러 A가 만든 프로그램은 10 / 5 = 2, 컴파일러 B가 만든 프로그램은 9 / 6 = 1.5
따라서 컴파일러 B가 만든 시퀀스를 사용하는 것이 더 효율적이다.
이를 통해 똑같은 컴퓨터로 똑같은 프로그램을 실행하더라도 어떤 컴파일러를 사용했느냐에 따라 CPU time도 달라질 수 있음을 알 수 있다.
또 CPI 는 '평균' 의 개념이 들어있기 때문에, CPI 가 작다고 무조건 더 성능이 좋다고 말할 수 없다.
일반적으로는 좋을지 몰라도, 어떤 특정 명령어가 많이 들어간 프로그램이 있다면, 그 명령어에 특화된 CPI 를 가진 컴퓨터가 실행 시간상에서 이점을 가질 수 있다.
또 컴파일러가 만든 명령어의 총 개수가 더 적다고 무조건 더 좋은 것도 아니다. Cycle이 적게 필요한 명령어를 많이 만들고 Cycle이 많이 필요한 명령어를 적게 만들었다면 총 개수가 많더라도 실행시간은 더 짧을 수 있다.
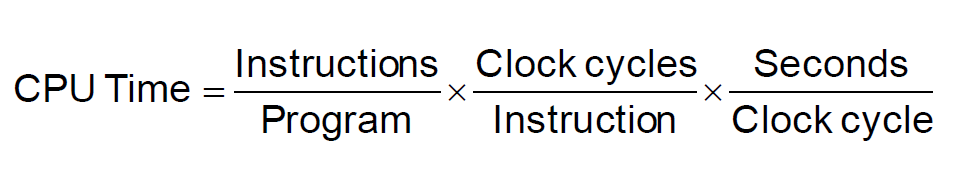
CPU 시간은 위와 같은 공식으로 계산될 수 있다.
따라서 명령어의 수가 많더라도 CPI 가 작으면 시간은 줄어들 수 있고, CPI 가 높더라도 전체 명령어의 수가 적다면 CPU Time 은 줄어들 수 있다.
CPU 성능과 벤치마크
벤치마크는 CPU 시간을 측정하는 프로그램이다.
이름이 벤치마크인 이유는 사람들이 자주 사용하는 대표적인 프로그램들을 모아서 그 프로그램들을 한번 실행시켜보기 때문이다.
대표적인 벤치마크 중 하나로 SPEC 이라는 벤치마크가 있다.
하지만 벤치마크의 의미가 요즘은 점점 줄어들고 있다.
그 이유로는
1. 프로그램이 너무 다양해서 대표적인 프로그램들의 실행시간으로 측정한 벤치마크가 좋다고, 내가 실행하려는 프로그램이 빠르게 실행된다는 보장을 하기 어렵고
2. CPU 제조사들이 벤치마크가 잘 나와야 잘 팔리니, 벤치마크 점수를 높이는데 집중해서 CPU를 설계하기 때문에, 우리가 원하는 프로그램이 빠르게 돌아지 않을 수 있다.
암달의 법칙 (Amdahl's Law)

어떤 작업을 수행하는데, 덧셈 로직이 많아서 30초의 시간이 걸린다고 해보자.
뺄셈과 관련된 로직은 20초, 곱셈은 25초, 나눗셈도 25초가 걸려서 총 100초가 걸린다고 해보자.
이때 내가 덧셈과 관련된 로직을 10배 개선해서 시간이 3초로 줄어들었다고 해보자.
그러면 총 시간이 73초로 27% 개선된다.
암달의 법칙은 '너가 덧셈 로직을 10배 개선했을 때, 과연 전체 프로그램도 10배 개선됐을까?' 를 물어보는 법칙이다.
위에서 보듯, 덧셈을 10배 개선했을 때 전체 로직은 27%의 개선밖에 되지 않았다. (이것도 물론 크지만)
따라서 내가 10배 개선한 덧셈 로직은 '덧셈' 에만 적용되고 나머지에는 영향을 미치지 않기 때문에, 프로그램의 총 개선시간을 계산할 때는, 아래와 같이 계산하도록 하는 것이 암달의 법칙이다.

(그리고 이와 관련된 MIPS 의 디자인 원칙이 '자주 사용하는 것을 빠르게 만들어라' 라는 원칙이다.)
이를 통해 우리는 자주 사용되는 중요한 로직을 1%라도 개선하는 것이, 중요하지 않은 로직을 20% 개선하는 것보다 더 큰 영향이 있음을 알 수 있다.
컴퓨터 분야에서 사용하는 단위

2의 거듭제곱 단위로 사용한다.
그런데 기존의 킬로, 메가, 기가 와 같은 단위가 10^3 단위로 증가하는 용도로 쓰이는 것과 다르다.
그래서 아래와 같은 용어를 쓰기도 한다.
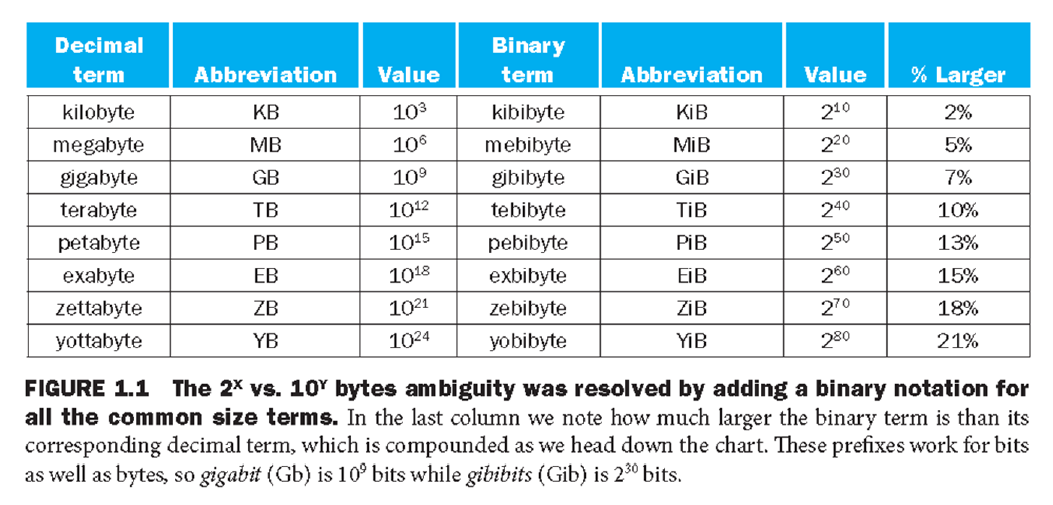
킬로바이트 대신에 '키비' 바이트로 부르는 방식이다.
'CS > 컴퓨터 구조' 카테고리의 다른 글
| [컴퓨터 구조] 10. Single Cycle MIPS - 개요 (0) | 2024.04.18 |
|---|---|
| [컴퓨터 구조] 9. 곱셈, 부동 소수점 (1) | 2024.04.17 |
| [컴퓨터 구조] 7. MIPS 명령어 총 정리 (0) | 2024.04.16 |
| [컴퓨터 구조] 6. MIPS Branch Instructions (0) | 2024.04.15 |
| [컴퓨터 구조] 5. MIPS Data Transfer Instructions (2) (0) | 2024.04.14 |
