문제 소개
https://www.acmicpc.net/problem/2376
2376번: 단말 정점들의 거리
첫째 줄에 단말 정점의 개수 n(2≤n≤1,000)이 주어진다. 다음 n-1개의 줄에는 차례로 1, 2번 단말 정점 사이의 거리, 2, 3번 단말 정점 사이의 거리, …, n-1, n번 단말 정점 사이의 거리가 주어진다. 다
www.acmicpc.net
이진트리와 인오더의 개념을 이용한 단순 구현 문제입니다.
규칙을 찾는다는 점에서 구성적 문제이기도 합니다.
문제를 어떻게 풀어야 할지는 알겠는데,
구현을 어떻게 할 지 감이 안잡히는 느낌으로 풀었던 문제입니다.
풀이 아이디어
풀이 아이디어는 생각보다 간단합니다.
문제에서 주어진 조건들을 하나씩 살펴보겠습니다.
1. n개의 단말 정점을 갖는 루트가 있는 이진 트리
이진 트리이므로, 자식은 최대 2개가 가능합니다.
2. 주어진 트리를 인오더로 탐색하였을 때,
단말 정점들이 나오는 순서대로 단말 정점들에 1, 2, …, n의 번호가 붙어 있다.
표현을 멋있게 적었습니다만, preorder, inorder, postorder 어떤 방법으로 탐색하든지
언제나 왼쪽 단말 정점부터 차례대로 탐색하게 됩니다.
https://hongku.tistory.com/160
알고리즘 :: 이진트리와 순회 전위순회(preorder), 중위 순회(inorder), 후위 순회(postorder) C/C++ 구현
이진 트리 Binary Tree 부모와 자식으로 나눠져있는 트리 그래프 자식은 왼쪽자식(left child), 오른쪽 자식(right child)로 나눠진다. 이진트리는 분할정복 탐색 알고리즘으로, 빠른속도로 탐색이 가능하
hongku.tistory.com
이 글의 예제를 보면 시각적으로 빠르게 이해됩니다.
3. 어떤 정점에 자식 정점이 있다면, 그 정점은 반드시 두 개의 자식 정점을 갖는다
1번 조건과 합치면 이 트리의 임의 노드는 자식을 갖지 않거나, 반드시 자식을 2개 갖습니다.
즉, 단말노드가 아닌 노드는 언제나 자식노드를 2개 갖고 있습니다.
이 3가지 조건을 만족하는 트리들을 그려보면서 규칙을 찾으면 됩니다.
저는 예제를 잘 줬다고 생각하는게, 단말노드가 4개일 때 가능한 케이스들을 그려놓다보면 규칙이 보입니다.
규칙 1 : 거리가 2인 두 단말노드는, 같은 부모 노드를 갖는다.
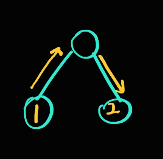
1번 노드와 2번 노드 사이의 거리는 2입니다.이 문제에서 이 경우 말고 거리가 2가 되는 노드 구성은 존재할 수 없습니다.
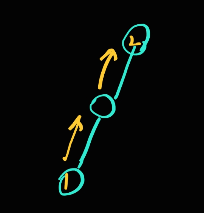
이런건 안됩니다. 반드시 자식은 2개를 가져야 합니다.(애초에 이 그림에서 2번 노드는 단말노드도 아니구요)
규칙 2 : 거리가 2인 구성의 단말 노드의 부모로 올라가면
거리가 2인 구성의 단말 노드와 인접했던 단말노드들의 거리는 1씩 줄어든다.
문제의 예제 입력 1을 그래프로 그려보면 다음과 같습니다.
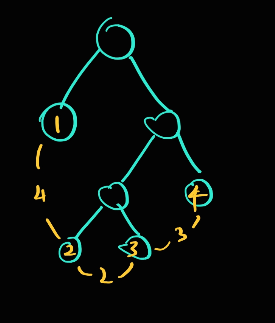
base case 인 거리가 2인 두 단말 노드에 대해서 처리가 끝났다고 생각하고,
그 부모 노드를 단말노드처럼 생각해서 보면

이렇게 오른쪽은 거리가 2인 단말 노드 구성이 되고, 왼쪽 노드와의 거리는 3이 되는데요.
기존 단말노드와의 양옆 거리가 1씩 줄어들었음을 알 수 있습니다.
이 두가지 규칙을 이용하면 임의의 두 노드에 대해서 거리를 구할 수 있습니다.
한번 '그래프를 그린다' 라는 관점으로 접근해보겠습니다.
그럼 그래프는 아래와 같은 방법으로 그릴 수 있습니다.
1. 거리가 2인 단말노드를 찾는다.
2. 둘의 부모 노드를 만들어서 둘과 연결한다.
3. 부모노드를 단말노드처럼 생각하고, 다시 거리가 2인 단말 노드를 찾는다.
4. 그들의 부모노드를 만들어서 연결한다.
5. 그들의 부모노드를 단말 노드처럼 생각하고 다시 거리가 2인 단말 노드를 찾는다.
(이하 반복)
이제 문제는 이걸 어떻게 구현하느냐겠죠..
사실상 이 구현 난이도 때문에 이 문제가 플레티넘까지 올라왔다고 생각합니다 ㅋㅋ
방법은 다양하게 있겠지만, 저는 두가지를 떠올렸습니다.
1. 위에 말한 것처럼 진짜 그래프를 구성하고
문제에서 요구하는 노드부터 시작해서 목적지 노드까지 DFS/BFS를 수행하여 거리를 계산한다.
2. 부모노드를 찾아서 만들 때마다 거리가 항상 1씩 균등하게 줄어드는 점을 이용해
DP처럼 매 순간에 각 노드마다 거리를 저장해둔다.
그 중 저는 2번 방식으로 구현했습니다.
구현 방법은 아래와 같습니다.
아래 3가지 배열을 준비합니다.
1. 임의의 단말노드 쌍에 대한 거리를 저장할 배열
2. 한 노드가 가진 자식 노드들과, 자신부터 자식노드들까지의 거리를 저장하는 배열
3. 인접한 단말 노드간 거리를 저장하는 배열
이때 단말 노드간 거리를 입력받는데, 거리의 기준은 왼쪽 노드를 기준으로 했습니다.
예를 들어 2 3 4 라고 입력받았다면, 인덱스가 0인 거리 '2'는 0번 노드와 1번 노드사이의 거리로 생각했습니다.
<전처리>
1번 배열은 2차원 배열로 만듭니다. array[from][to] = distance 를 의미합니다.
2번 배열도 2차원 배열로 만듭니다.
각각의 노드마다 [ [ 노드번호, 부모와의 거리 ] ] 꼴로 배열을 만들어 둡니다.
단말 노드는 가진 자식이 없지만, [ [자신노드번호, 0] ] 형태로 저장해둡니다.모두 언젠가는 어떤 노드의 자식이 될 테니 미리 저장해 둡니다.
1. 단말 노드간 거리를 입력받아 3번 배열에 순서대로 넣는다.
2. 0번부터 차례대로 단말 노드간 거리를 체크한다.
<while문으로 반복 : 종료 조건은 인덱스가 3번 배열의 인덱스 범위를 벗어난 경우>
3-1. 만약 현재 인덱스에서 단말 노드간 거리가 2라면
4. 왼쪽 단말 노드의 자식들에 대해, 부모노드와의 거리를 1 증가시킨다.
5. 오른쪽 단말 노드의 자식들에 대해, 부모노드와 의 거리를 1 증가시킨다.
6. 오른쪽 단말 노드의 자식들을 왼쪽 단말 노드의 자식들에 더한다.
7. 오른쪽 단말 노드를 제거한다.
(이 과정을 통해, 두 단말노드의 부모노드를 하나의 단말노드처럼 볼 수 있게 되었습니다.)
(또한 두 단말노드를 합친 후에도, 현재 인덱스는 부모노드를 가리키는 인덱스로 기능합니다.)
(이 과정은 위에 적었던 2번 배열에 대해 처리합니다.)
8. 현재 인덱스의 단말 노드 왼쪽과 인접한 단말 노드의 거리를 1 줄입니다.
9. 현재 인덱스의 단말 노드 오른쪽과 인접한 단말 노드의 거리를 1 줄입니다.
10. 현재 인덱스의 단말노드 거리를 제거합니다.
(이 과정을 통해, 부모 노드를 단말 노드로 보았을 때, 인접한 양 옆의 노드 거리를 1씩 줄였습니다.)
(이 과정은 위에 적었던 3번 배열에 대해서 처리합니다.)
11. (단말 노드처럼 만든) 부모노드에 인접한 왼쪽의 단말노드에 속한 자식들과,
부모노드에 속한 자식들 사이의 거리를 구해 1번 배열에 저장합니다.
12. 부모노드에 인접한 오른쪽의 단말 노드의 자식들과
부모노드에 속한 자식들 사이의 거리를 구해 1번 배열에 저장합니다.
(거리는 왼쪽 단말 노드를 기준으로
왼쪽 단말 노드에 속한 자식과 왼쪽 단말 노드사이의 거리
+ 왼쪽 단말 노드와 부모노드사이 거리
+ 부모노드와 부모노드의 자식 사이의 거리
이렇게 3부분으로 나누어 구합니다. 복잡하죠.. 오른쪽도 같은 방식으로 구하면 됩니다.)
(이렇게 현재 노드에 대해서 모든 처리가 끝났으니,
다시 단말노드 사이의 거리가 2인 단말노드를 찾으면 됩니다.)
13. 현재 단말 노드와, 인접한 왼쪽 단말 노드 사이의 거리가 2라면 인덱스를 1 감소합니다.
(인덱스는 왼쪽 노드를 기준으로 하기 때문입니다.)
3-2 만약 현재 인덱스에서 단말 노드간 거리가 2가 아니라면 인덱스를 1 증가시킵니다.
<반복문 범위>
이 반복문이 끝나있다면, 이제 어떤 임의의 두 단말 노드 사이의 거리에 대해서도 모두 구할 수 있습니다.
여기서 성능을 조금 더 올린다면 거리를 구할 때 중복해서 구하지 않도록,
이미 구한 거리는 갱신하지 않게 할 수도 있습니다.
14. 구하고자 하는 두 단말노드의 번호를 입력받고, 1번 배열에서 값을 찾아 출력한다.
이것이 구현 알고리즘 입니다 ㅋㅋ
길고.. 복잡하네요..
소스 코드
n = int(input())
# 1번 배열
distance_table = [[0 for _ in range(n)] for _ in range(n)]
# 2번 배열
# i 번째 단말 노드는 초기에 자기 자신인 i를 자식으로 갖고 있고, 자신과 자식사이의 거리는 0이다.
children = [[[i, 0]] for i in range(n)]
# 3번 배열
distance = []
for i in range(n - 1):
d = int(input())
distance.append(d)
distance_table[i][i + 1] = d
i = 0
while True:
if i == len(distance):
break
# distance[i] => i, i+1 사이의 거리 (왼쪽 기준 정렬)
if distance[i] == 2:
# (i, i+1) 사이의 거리가 2라면, 이 둘은 같은 부모를 둔 자식 노드이므로,
# "(i-1, i) 사이의 거리 - 1" 이 (i-1, 부모) 사이의 거리이고,
# "(i, i+1) 사이의 거리 - 1" 이 (부모, i+1) 사이의 거리이다.
# 부모를 단말노드로 보고 거리가 2로 줄어든 것에 대해 이 과정을 반복한다.
# 그리고 이 과정을 진행하는 동안 임의의 두 단말노드쌍 (a, b) 사이의 거리 표를 채운다.
# n 은 1000 이므로 O(n^2)에 대해서 이 문제를 해결할 수 있다.
# 부모와 자식 사이의 거리를 1 늘려준다.
for j in range(len(children[i])):
children[i][j][1] += 1
if i+1 < len(children):
for j in range(len(children[i + 1])):
children[i + 1][j][1] += 1
# i번째 노드를 기준으로, 이제 children[i] 와 children[i+1] 이 부모 노드의 자식들이다.
children[i] += children[i + 1]
# children[i+1] 은 필요가 없다.
children.pop(i + 1)
# 좌우의 distance를 조절한다.
if i > 0:
distance[i - 1] -= 1
if i+1 < len(distance):
distance[i + 1] -= 1
# 현재 distance는 필요 없으니 삭제
distance.pop(i)
# distance_table 을 채운다. => i-1 번째 아이들과 i번째 아이들 각각의 거리, i번째 아이들과 i+1번째 아이들 각각의 거리를 채운다.
if i > 0:
for k in range(len(children[i - 1])):
_from = children[i - 1][k][0]
_from_distance_from_parent = children[i - 1][k][1]
for m in range(len(children[i])):
_to = children[i][m][0]
if distance_table[_from][_to] > 0:
continue
distance_from_parent = children[i][m][1]
distance_table[_from][_to] = _from_distance_from_parent + distance[i - 1] + distance_from_parent
if i+1 < len(children):
for k in range(len(children[i])):
_from = children[i][k][0]
_from_distance_from_parent = children[i][k][1]
for m in range(len(children[i + 1])):
_to = children[i + 1][m][0]
if distance_table[_from][_to] > 0:
continue
distance_from_parent = children[i + 1][m][1]
distance_table[_from][_to] = _from_distance_from_parent + distance[i] + distance_from_parent
# 만약 부모 노드의 왼쪽이 거리가 2가 되었다면, 인덱스를 하나 감소하여 반복문을 진행한다.
if i > 0 and distance[i - 1] == 2:
i -= 1
else:
i += 1
find_from, find_to = map(int, input().split())
print(distance_table[min(find_from, find_to) -1][max(find_from, find_to) -1])
주석이 많아서 길어보이지만, 이렇게라도 안쓰면 복잡해서 정리가 안되더라구요..
주석으로 코드상에 구현 계획과 구체적인 설정을 적어두면
구현 중 헷갈리거나 실수로 빼먹는 부분이 생기지 않도록 하는데도 도움이 되는 것 같습니다.
블로그에서 처음으로 어려운 난이도의 구현 문제를 정리해보았습니다.
구현 문제가 어려워지면, 정말 복잡해져서 설명하기도 쉽지 않은 것 같네요 ㅋㅋ
(사실 플레티넘의 구현문제는 구현을 어떻게 할 지 감이 안잡히는 문제보다,
예외가 안생기게 꼼꼼하게 구석구석 구현하는게 어려운 것 같습니다.)
'알고리즘 (PS) > BOJ' 카테고리의 다른 글
| [백준] 20936 - 우선순위 계산기 (P4) (0) | 2021.08.18 |
|---|---|
| [백준] 20129 - 뒤집힌 계산기 (G3) (2) | 2021.08.17 |
| [백준] 11054 - 가장 긴 바이토닉 부분 수열 (G3) (0) | 2021.08.10 |
| [백준] 14653 - 너의 이름은 (0) | 2021.08.07 |
| [백준] 9465 - 스티커 (0) | 2021.07.29 |
